Την ώρα που η προσφορά των αρχαίων Ελλήνων στους τομείς της λογικής σκέψης, της επιστήμης και των καλών τεχνών παραμένει αξεπέραστη, η ιστορία της αρχαιοελληνικής τεχνολογίας παραμένει εν πολλοίς άγνωστη, ακόμα και σε μας.
Τα απίστευτα τεχνολογικά επιτεύγματα των προγόνων μας φαίνεται να έχουν υποχωρήσει κάτω από το πελώριο βάρος των κολοσσιαίων συνεισφορών τους σε αυτό που ονομάζουμε γέννηση του σύγχρονου κόσμου, αν και αυτό μόνο άδικο μπορεί να χαρακτηριστεί.
Γιατί οι αρχαίοι ημών πρόγονοι έκαναν τη μεγάλη πολιτισμική διαφορά και στον τομέα της τεχνολογίας, αφήνοντας παγκόσμια κληρονομιά ένα πρωτάκουστο τεχνολογικό θαύμα που όμοιό του δεν υπήρχε στον τότε γνωστό κόσμο.
Εδώ δεν θα μιλήσουμε φυσικά για τη συνωμοσιολογική «απόκρυφη τεχνολογία» των Ελλήνων, καθώς αυτές οι ιστορίες γι’ αγρίους το μόνο που κάνουν είναι να συσκοτίζουν τη λαμπρή παρακαταθήκη του ελληνικού πολιτισμού. Οι αρχαίοι δεν είχαν εξάλλου ανάγκη από «μυστικές τεχνολογίες», καθώς οι φανερές τους έφταναν και περίσσευαν για να τους στέψουν πρωτομάστορες ενός κόσμου που ερχόταν ολοταχώς να κόψει δεσμούς με τα παλιά και να βάλει τα πρώτα θεμέλια αυτού που θα ονομαζόταν αργότερα δυτικός πολιτισμός.
Τα τεχνολογικά δημιουργήματά τους είχαν εξάλλου την οσμή του απόκοσμου, καθώς πώς μπορείς να ισχυριστείς σε κάποιον ότι οι αρχαίοι Έλληνες είχαν ρομπότ-υπηρέτριες, κινηματογράφο, αυτόματα ρολόγια και αναλογικούς υπολογιστές και να μη σε κοιτάξει σαν εξωγήινο!
Κι όμως, η ενδελεχής μελέτη της αρχαιοελληνικής, λατινικής και αραβικής γραμματείας, των αγγειογραφικών πληροφοριών και των λιγοστών σχετικών αρχαιολογικών ευρημάτων υποδεικνύουν έναν κόσμο γεμάτο από τεχνολογικά καλούδια που θα ζηλεύαμε ενδεχομένως ακόμα και σήμερα.
Η σχετικά άγνωστη αυτή πτυχή του αρχαιοελληνικού πολιτισμού φανερώνει πράγματι ότι η τεχνολογία αιχμής των αρχαίων Ελλήνων, εκεί στα τέλη του αρχαιοελληνικού κόσμου, ήταν εξαιρετικά όμοια με τις απαρχές της σύγχρονης δυτικής τεχνολογίας. Κοχλίες και περικόχλια, οδοντωτοί τροχοί, κανόνες, τροχαλίες, ιμάντες, αλυσίδες και βαλβίδες επιστρατεύτηκαν για να φτιάξουν όλων των λογιών τα gadgets, αποτελώντας τον θεμέλιο λίθο της πολύπλοκης ελληνικής τεχνολογίας. Και την ίδια τη βάση για τη σύγχρονη τεχνολογική περιπέτεια φυσικά, καμιά αμφιβολία!
Μετά το τέλος του ελληνικού κόσμου, η ανθρωπότητα θα χρειαζόταν περισσότερα από χίλια χρόνια για να επανακτήσει την αξιοθαύμαστη και λησμονημένη τεχνολογία των αρχαίων Ελλήνων. Πάνω της πάτησε, υιοθετώντας τη ανέξοδα και απροβλημάτιστα, και ανοίχτηκε με θάρρος σε αυτό που θα ονομαζόταν σύγχρονη επιστήμη, αντλώντας από τους Έλληνες τις ίδιες τις εννοιολογικές βάσεις του δυτικού τεχνολογικού πολιτισμού.
Περισσότερες από 300 εφευρέσεις των Ελλήνων είναι σήμερα γνωστές και όλες τους σε κάνουν να ξύνεις το κεφάλι σου για τα πώς και τα γιατί της ύπαρξής τους: από το «ρομπότ-υπηρέτρια» του Φίλωνα, τον υδραυλικό τηλέγραφο του Αινεία και τον «κινηματογράφο» του Ήρωνα μέχρι το αυτόματο ωρολόγιο του Κτησίβιου, τον αστρολάβο του Πτολεμαίου και τον αναλογικό υπολογιστή των Αντικυθήρων, οι έλληνες τεχνουργοί πάτησαν πάνω στους πρωτοπόρους μαθηματικούς, γεωγράφους, αστρονόμους και φιλοσόφους και σκάρωσαν εφευρέσεις που έμελλε να γίνουν τα δομικά χαρακτηριστικά της μοντέρνας τεχνολογίας.
Ήταν όμως και οι ίδιοι οι επιστήμονες που έβρισκαν πρακτικές εφαρμογές στις θεωρίες τους, δημιουργώντας έναν εκρηκτικό τεχνολογικό κόσμο που παλλόταν από εφευρέσεις, αυτόματα και υπολογιστές, λες και ξεπήδησε από σελίδες επιστημονικής φαντασίας. Πλάτωνας (ξυπνητήρι), Αριστοτέλης (ρολόι-ξυπνητήρι), Πυθαγόρας (κούπα), Αρχιμήδης (υδραυλικό ωρολόγιο), Αρχύτας (πτητική συσκευή) μπόλιασαν την τεχνολογία με θαυμαστά έργα, δίνοντας την ιδανική πάσα στους αλεξανδρινούς μηχανικούς να γεμίσουν τον κόσμο με καταπληκτικά «μαγικά» αυτόματα τεχνουργήματα, ρομπότ, «κινηματογράφο», «αυτοκίνητο-κουκλοθέατρο» και άλλα πολλά εξώκοσμα μαραφέτια.
Η ελληνική τεχνολογία απλώθηκε πάνω σε όλους τους τομείς του επιστητού και αφορούσε, πέρα από τα θρυλικά «αυτόματα», τα αστρονομικά ρολόγια (αστρολάβος, τετράντας κ.λπ.) και τους μετρητικούς μηχανισμούς (διόπτρες, αλφάδια, οδόμετρα, ναυτικά δρομόμετρα, ποδοκίνητους τόρνους, παντογράφους, γωνιόμετρα, ανεμολόγια, τρύπανα, εσωτερικούς σπειροτόμους κ.λπ.), σε ιατρική τεχνολογία («Πυουλκός», η σύριγγα δηλαδή), αγροτική (ελαιοτριβεία, μύλοι, πρέσες λαδιού και άροτρα), υφαντική («Αργαλειός της Πηνελόπης»), αθλητική (Ύσπληγα και Ιππάφεση), μηχανική (γερανοί, ανυψωτικά μηχανήματα, πολύσπαστα, βαρούλκα, σύνδεσμοι, γόμφοι και εμπόλια), υδραυλική (Κηλώνιον, αλυσιδωτές αντλίες, υδραυλικοί τροχοί, πυροσβεστικές αντλίες, φυσερά και αεραντλίες), αλλά και τηλεπικοινωνίες (Πυρσεία και Φρυκτωρίες, υδραυλικοί και ακουστικοί τηλέγραφοι, κρυπτογραφικοί δίσκοι), πολιορκητικές συσκευές (Αιωρούμενος Κριός του Γήρα, Χελώνη Επίχωσης του Διάδη, Ελέπολις του Επιμάχου, Σαμβύκη του Δαμίου, Φλογοβόλο των Βοιωτών, Γαστραφέτης, αλλά και τα πάμπολλα είδη καταπέλτη) και τόσα ακόμα!
Το Μουσείο Αρχαίας Ελληνικής Τεχνολογίας «Κώστας Κοτσανάς», που εδρεύει στο Κατάκολο Ηλείας από το 2003, φιλοξενεί την απίστευτη τεχνολογία των προγόνων μας, η οποία καλύπτει μια μακρά περίοδο από το 2000 π.Χ. μέχρι και το τέλος του ελληνικού κόσμου. Ο Κώστας Κοτσανάς, έπειτα από την 25χρονη έρευνά του, κατάφερε να ανασυγκροτήσει την εγκυρότερη και πληρέστερη έκθεση για την αρχαία ελληνική τεχνολογία. Όλες οι φωτογραφίες των αρχαιοελληνικών τεχνολογιών προέρχονται από το υπέροχο μουσείο του.
Κι αν ο υπολογιστικός μηχανισμός των Αντικυθήρων, ο φορητός υπολογιστής της αρχαιότητας και η πρώτη ποτέ αναλογική υπολογιστική μηχανή του κόσμου που χρησιμοποιούνταν για τον καθορισμό και την πρόβλεψη σημαντικών αστρονομικών και ημερολογιακών γεγονότων, παραείναι δημοφιλής για να αναλυθεί, ώρα να ανακαλύψουμε μερικές μόνο από τις κολοσσιαίες σε σύλληψη και εκτέλεση τεχνολογικές συνεισφορές της αρχαίας Ελλάδας…
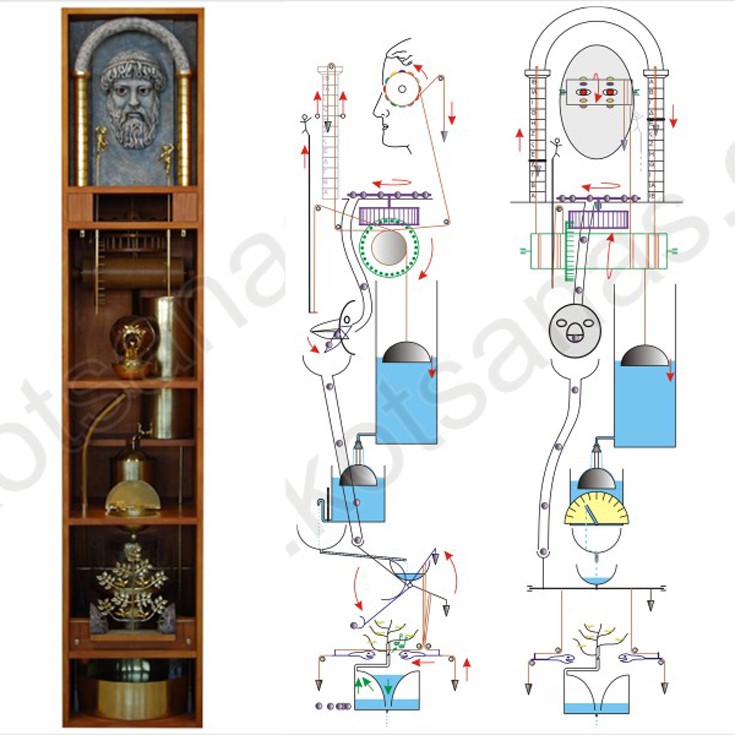
O «Κινηματογράφος» του Ήρωνα
Το σταθερό αυτόματο θέατρο του Ήρωνα, που οι αρχαίοι Έλληνες ονόμαζαν απλώς «κινηματογράφο», ήταν άλλη μια ξακουστή εφεύρεση της πολυσχιδούς αυτής προσωπικότητας από την Αλεξάνδρεια. Ο Ήρων ο Αλεξανδρεύς ήταν πολυπράγμων μηχανικός, άριστος μαθηματικός και μοναδικός εφευρέτης που δικαίως χαρακτηρίστηκε «Ντα Βίντσι της αρχαιότητας», όταν δεν λειτουργούσε φυσικά ως θαυματοποιός και μαέστρος των τεχνασμάτων.
Στο βιβλίο του «Πνευματικά», ο Ήρωνας περιγράφει ογδόντα περίπου αυτοματισμούς, πρακτικές εφαρμογές δηλαδή όλων των τότε γνωστών αρχών των φυσικών επιστημών, και στο επόμενο σύγγραμμά του «Αυτοματοποιητική» μας αφηγείται το «κινητό αυτόματο» (ένα αυτοκινούμενο προγραμματιζόμενο όχημα) και το εκπληκτικό «στατόν» αυτόματο θέατρο, τον κινηματογράφο των αρχαίων Ελλήνων δηλαδή με κινούμενη εικόνα και ήχο!
Στα πρώιμα κινούμενα σχέδια του Ήρωνα μπορούσε κάποιος να παρακολουθήσει όλο τον Μύθο του Ναυπλίου, ο οποίος αποζητά να εκδικηθεί τους Αχαιούς που σκότωσαν τον γιο του Παλαμήδη στην Τροία. Η αυλαία ανοιγόκλεινε, μορφές κινούνταν, ήχοι παράγονταν, σκηνικά άλλαζαν, φωτιές άναβαν, κεραυνοί έπεφταν, βροντές ακούγονταν και πολλά ακόμα, τα οποία συνέβαιναν αυτόματα! Το «στατόν» θέατρο συνεχίζει να προβληματίζει τους σύγχρονους μηχανικούς του αυτοματισμού για τον περίπλοκο και αρμονικό τρόπο λειτουργίας του. Ο Ήρων βελτίωσε το σταθερό αυτόματο θέατρο του Φίλωνος του Βυζαντίου (3ος αιώνας π.Χ.) αποδίδοντας ένα πραγματικό θαύμα του θεάματος. Όλα μάλιστα γίνονταν αυτόματα με το τράβηγμα του σχοινιού της πρόσοψης (ή -όπως θα λέγαμε σήμερα- με το πάτημα ενός κουμπιού)…
Το «πουλί που κελαηδά» του Ήρωνα
Οι αρχαίοι το έλεγαν «Περιστρεφόμενο Φθεγγόμενο Μελαγκόρυφο» και δεν ήταν παρά μια λάρνακα ναού που παρουσίαζε ένα πουλί να περιστρέφεται αυτόματα και να κελαηδά όταν ο επισκέπτης γυρνούσε τον εξωτερικό τροχό της θήκης του. Δύο άξονες, μια σειρά από ακτινωτούς τροχούς, ένας λυγισμένος αυλός και ένα αντεστραμμένο κοίλο δοχείο που βυθιζόταν στο νερό έκαναν όλο το μαγικό.
Το πουλί περιστρεφόταν ταχύτατα και τιτίβιζε με φθόγγους μεταβαλλόμενης συχνότητας, ώστε να αποδίδεται πιστά το πραγματικό κελάηδισμα διάφορων ειδών!
Η «φιλοσοφική λίθος» του Ήρωνα
Άλλη μια απίστευτη επινόηση του Ήρωνος του Αλεξανδρέως, αυτή λειτουργούσε ως καθαρό ταχυδακτυλουργικό τρικ, μιας και ο σκοπός της ήταν να μεταποιεί ένα υγρό σε κάποιο άλλο (συνήθως τον οίνο σε νερό)! Στη «φιλοσοφική λίθο» έριχνες νεράκι και έπαιρνες ίσης ποσότητας κρασί και τανάπαλιν, όπως μας λέει ο πανεπιστήμων στα «Πνευματικά» του.
Το «αυτόματο σπονδείο με κερματοδέκτη» του Ήρωνα
Απλά απλά, μιλάμε για τον πρώτο αυτόματο πωλητή της Ιστορίας! Ο πιστός έριχνε ένα πεντάδραχμο κέρμα στο αγγείο και έπαιρνε αυτόματα αγιασμό. Όπως μας λέει ο Ήρων στα «Πνευματικά», το νόμισμα έπεφτε πάνω στον δίσκο ενός ζυγού και με την εκτροπή του δίσκου από τη θέση του, άνοιγε μια κωνική βαλβίδα που απελευθέρωνε αντίστοιχη (του βάρους του νομίσματος) ποσότητα αγιασμένου ύδατος…
Η Αιολόσφαιρα του Ήρωνα
Πολύ πριν από τον Τζέιμς Βατ και τη Βιομηχανική του Επανάσταση, ο Ήρων ο Αλεξανδρεύς είχε στα χέρια του την πρώτη ατμομηχανή της ανθρωπότητας! Και πάλι στα «Πνευματικά», ο σπουδαίος επιστήμονας μας λέει πως πάνω από τον λέβητα υπήρχαν δύο σωλήνες και γύρω από τα καμπυλωμένα άκρα τους εδραζόταν μια σφαίρα με δύο ακροφύσια. Όταν θερμαινόταν το νερό του λέβητα, ατμοποιούνταν και -περνώντας από τους δύο κατακόρυφους σωλήνες- εισερχόταν στη σφαίρα και εξερχόταν με ορμή από τα δύο ακροφύσια, εξαναγκάζοντάς τη σφαίρα σε (αντίθετης διεύθυνσης) συνεχή περιστροφή.
O πρόδρομος της ατμομηχανής λίγο έλειψε να φέρει τη Βιομηχανική Επανάσταση στα ελληνιστικά χρόνια, καθώς το μόνο που της έλειπε ήταν μια τροχαλία για τη μετάδοση της κίνησης. Η πρώιμη αυτή τεχνολογική επανάσταση δεν θα συντελούνταν βέβαια ποτέ, καθώς τον πρώτο λόγο ήταν έτοιμοι να πάρουν οι Ρωμαίοι…
Η μαγική κρήνη του Ήρωνα
Εδώ ο Ήρωνας πάντρεψε και πάλι επιστημονική γνώση, τεχνολογική καινοτομία και ολίγον από showbiz, σκαρώνοντας μια ευφυέστατη κρήνη που παραβίαζε φαινομενικά τις αρχές της υδροστατικής πίεσης και των συγκοινωνούντων δοχείων! Κι αυτό γιατί εκτόξευε το νερό ψηλότερα από τη διαθέσιμη στάθμη της δεξαμενής της.
Με έναν δαιμόνιο μηχανισμό αναπλήρωσης του υγρού και την επιστράτευση της αρχής του εγκλωβισμένου αέρα, όπως μας αποκαλύπτει στα «Πνευματικά», ο Ήρωνας μάγευε το κοινό της εποχής με τα παράδοξά του. Η κρήνη εκτόξευε το νερό ψηλότερα απ’ όσο όφειλε και το έκανε μάλιστα αυτόματα, καθώς η διαδικασία ήταν αυτοσυντηρούμενη και συνέχιζε μέχρι να αδειάσει πλήρως η δεξαμενή…
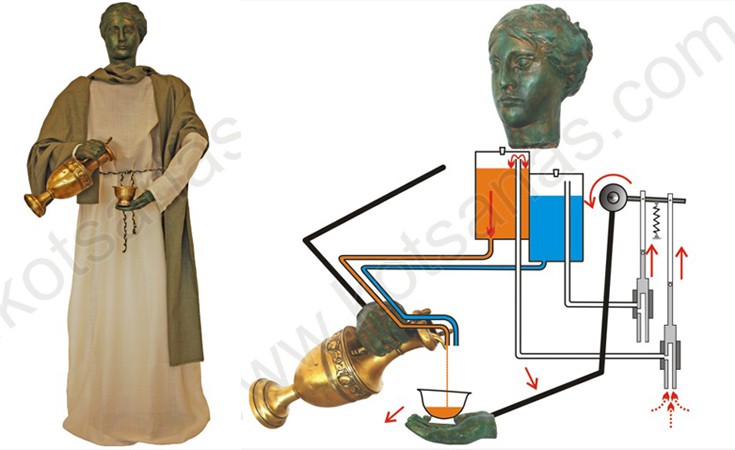
Το «ρομπότ-υπηρέτρια» του Φίλωνα
Η αυτόματη υπηρέτρια του Φίλωνα είναι πράγματι το πρώτο λειτουργικό ρομπότ της ανθρωπότητας! Δεν ήταν παρά ένα ανθρωποειδές σε φυσικό μέγεθος που κρατούσε στο δεξί του χέρι μια οινοχόη. Όταν ο χρήστης τοποθετούσε ένα κύπελλο (κρατήρα) στην παλάμη της «θεραπαινίδας», εκείνη έριχνε αυτόματα κρασί και δευτερευόντως παρείχε επιλογή για ανάμειξη με νερό, κατά την επιθυμία του κύρη της!
Στο εσωτερικό της υπηρέτριας βρίσκονταν δύο στεγανά δοχεία, ένα με κρασί και ένα με νερό, και μέσω ενός πολύπλοκου αρθρωτού μηχανισμού γινόταν όλη η αυτοματοποιημένη δουλειά. Όταν μισογέμιζε το κύπελλο με κρασί, το χέρι κατέβαινε περισσότερο (λόγω βάρους) και η ροή του οίνου σταματούσε. Αν ήθελες (αν συνέχιζες δηλαδή να αφήνεις το κύπελλο στο χέρι της κοπέλας), έρρεε νερό ώστε να αραιώσεις το κρασί σου, κατά την προσφιλή συνήθεια των αρχαίων.
Η υπηρέτρια γέμιζε το κύπελλο με καθαρό οίνο ή αραιωμένο με νερό στην ποσότητα που επιθυμούσες ανάλογα με τη χρονική στιγμή που θα τραβούσες τον κρατήρα από την παλάμη της. Απίστευτο κι όμως αληθινό…
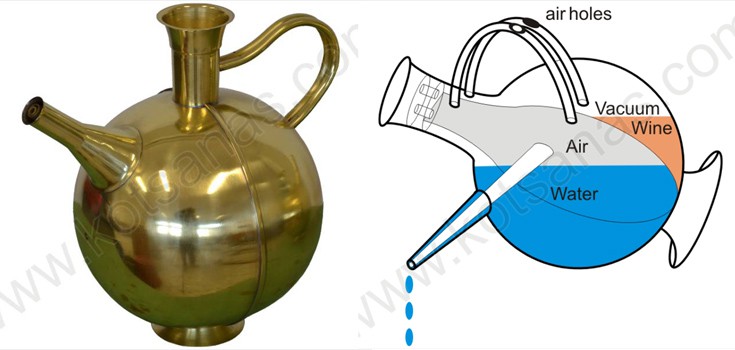
Η ευφυής οινοχόη του Φίλωνα
Την έχουν χαρακτηρίσει ως την πρώτη ποτέ «έξυπνη» συσκευή οικιακής χρήσης στην παγκόσμια ιστορία και μάλλον έχουν δίκιο! Η λειτουργία της ήταν παρόμοια με το ρομπότ-υπηρέτρια, μόνο που εδώ μιλάμε για απλή οινοχόη. Ο Φίλων ο Βυζάντιος έφτιαξε λοιπόν τη «smart» κανάτα της αρχαιότητας, η οποία απελευθέρωνε αυτόματα νερό, κρασί ή νερωμένο κρασί ανάλογα με τη βούληση του οινοχόου.
Ένα κατακόρυφο διάφραγμα χώριζε την οινοχόη σε δύο διαμερίσματα (νερού και κρασιού) και ανάλογα με τις οπές αερισμού που κάλυπτε κάθε φορά ο οινοχόος με τα δάκτυλά του, η κανάτα έκανε όλο το μαγικό! Κάθε επιθυμία των συνδαιτυμόνων γινόταν αμέσως διαταγή για τη μαγική οινοχόη…
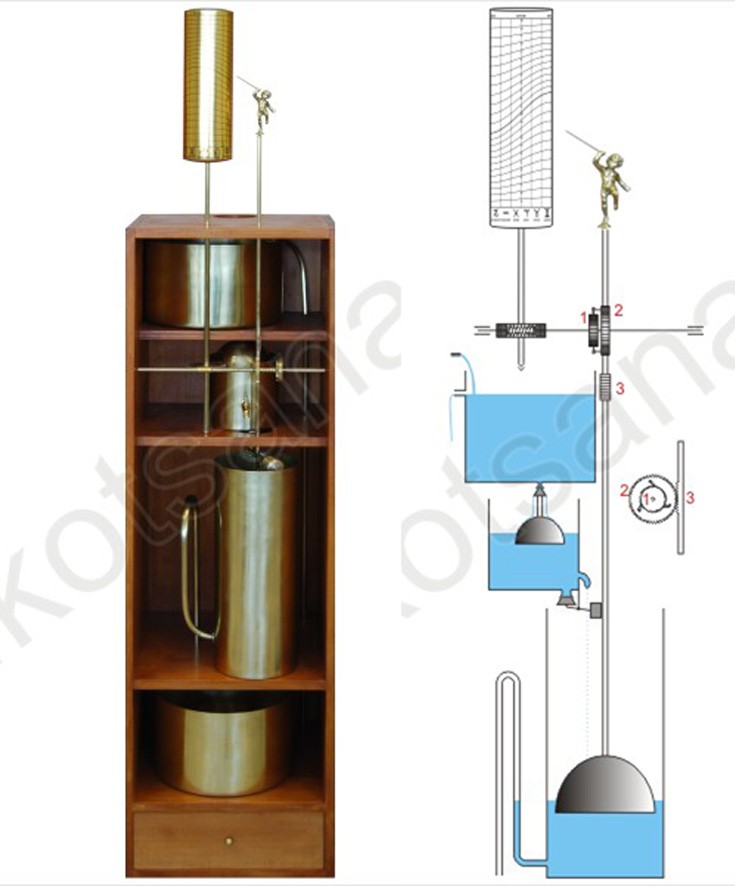
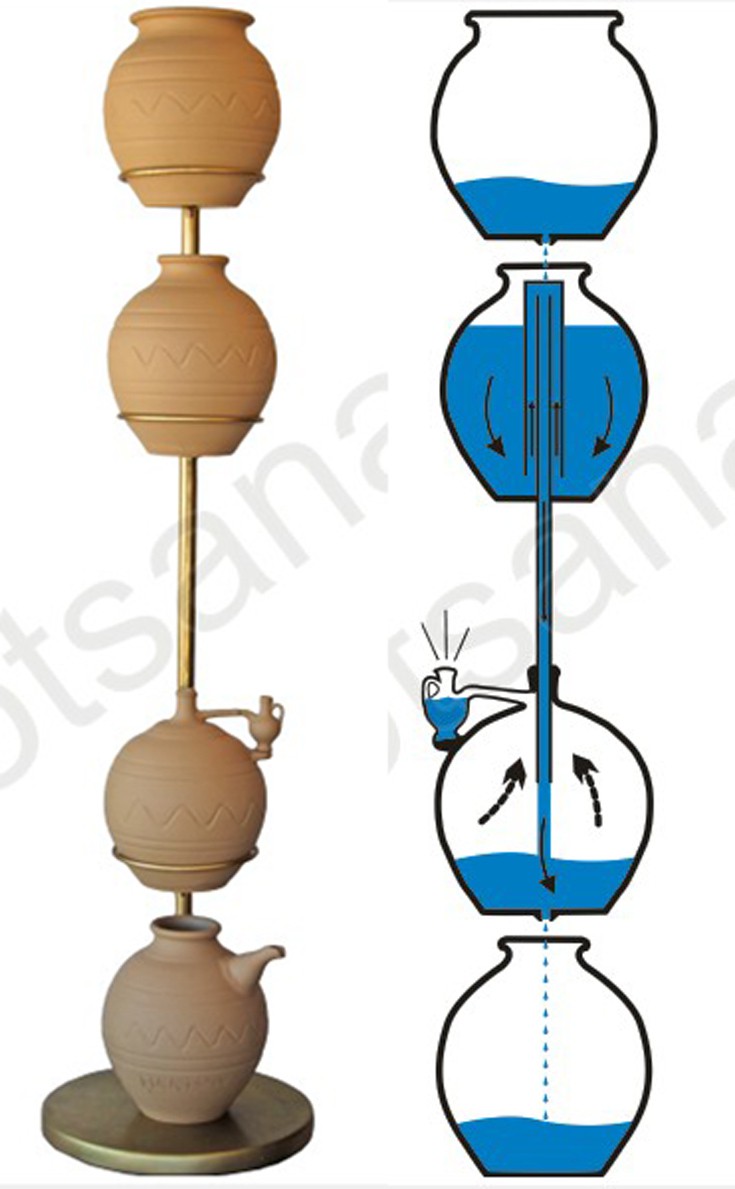
Το αυτόματο ωρολόγιο του Κτησίβιου
Το υδραυλικό ωρολόγιο του Κτησίβιου ήταν ένα θαύμα του αυτοματισμού με συνεχή λειτουργία χωρίς καμία ανθρώπινη παρέμβαση! Οι Έλληνες μαγεύτηκαν με τη μέτρηση του χρόνου και επινόησαν, από τον 6ο αιώνα π.Χ. ως το τέλος της αρχαιότητας, μια καταπληκτική συλλογή ρολογιών που χαρακτηρίζεται από απεριόριστη φαντασία, εκπληκτική ποικιλία, υψηλή αισθητική και εξαιρετική εργονομία φυσικά. Από ηλιακά (σκιαθηρικά) ρολόγια, που έδειχναν την ώρα με βάση τη σκιά πάνω σε ειδικά βαθμονομημένη επιφάνεια, μέχρι και υδραυλικά ρολόγια (κλεψύδρες), που στηρίζονταν στη σταθερή και συνεχή ροή ύδατος ανάμεσα σε δύο δοχεία, οι αρχαίοι έκαναν κυριολεκτικά θαύματα στη μέτρηση του χρόνου.
Κανένα βέβαια δεν ήταν σαν το αυτόματο ρολόι του Κτησίβιου, που μπορούσε να λειτουργεί αδιάκοπα χωρίς καμία ανθρώπινη παρέμβαση, υποδεικνύοντας τα 365 διαφορετικά ωράρια του έτους! Ένα ευφυές σύστημα δοχείων συνδεόταν σε μια πηγή νερού και μέσω βαλβίδων ασφαλείας και ελεγκτών στάθμης υδάτων κινούνταν ο δείκτης, ο οποίος υποδείκνυε την ώρα του 24ώρου σε ένα περιστρεφόμενο τύμπανο που περιείχε το διάγραμμα των ωρών της ημέρας και της νύχτας, ανάλογα με την ημερομηνία. Στο τέλος του 24ώρου, το νερό άδειαζε ταχύτατα και η διαδικασία επαναλαμβανόταν στο διηνεκές…
Το υδραυλικό ωρολόγιο του Αρχιμήδη
Το πρώτο ποτέ υδραυλικό ρολόι με χτύπους ήταν πνευματικό παιδί του μεγαλύτερου μαθηματικού του ελληνικού κόσμου. Ήταν ένα πολύπλοκο υδραυλικό ωρολόγιο με πολλά αυτόματα κινούμενα πάρεργα, τα οποία έκαναν τους δυο κίονες της πρόσοψης, μέσω αντίστοιχων κινούμενων δακτυλίων (και δύο αγαλματιδίων), να υποδεικνύουν τις ώρες που διανύονταν και τις ώρες που απέμεναν, αντίστοιχα.
Κάθε ώρα, οι κόρες των οφθαλμών ενός ανθρώπινου προσωπείου άλλαζαν χρώμα και ένα σφαιρίδιο έπεφτε με κρότο σε ένα δοχείο από το (αυτόματα) ανοιγόμενο ράμφος ενός κόρακα! Το νερό χυνόταν ταυτοχρόνως μέσα σε ογκομετρικό δοχείο και σε χρονικό διάστημα μίας ώρας ανατρεπόταν αυτόματα, οπότε δύο φίδια κινούνταν συρίζοντας προς τα πουλιά των δένδρων που σφύριζαν τρομαγμένα. Αυτός κι αν ήταν εντυπωσιακός τρόπος να μαθαίνεις την ώρα!
Το ξυπνητήρι του Αριστοτέλη
Ο Αριστοτέλης δεν ήθελε να περνά τη μέρα του στο κρεβάτι, καθώς δεν είχε χρόνο για ξόδεμα στην οδύσσειά του να αναλύσει λογικά τον κόσμο μας. Γι’ αυτό και αναγκάστηκε νε εφεύρει ένα υδραυλικό ρολόι-ξυπνητήρι ώστε να ξυπνά έπειτα από σύντομο χρονικό διάστημα ύπνου και να επιστρέφει γοργά στη μελέτη του. Η μαρτυρία διασώζεται στον Διογένη τον Λαέρτιο («Βίοι φιλοσόφων»), αν και δεν περιγράφει τη λειτουργία του μηχανισμού του, η οποία βασιζόταν ωστόσο στο αντίστοιχο ξυπνητήρι του Πλάτωνα.
Ένα δοχείο με νερό άδειαζε λοιπόν με προκαθορισμένο ρυθμό εκροής σε ένα άλλο δοχείο που έφερε έναν αρθρωμένο ημισφαιρικό πλωτήρα. Την προαποφασισμένη στιγμή που γέμιζε το δοχείο, ο πλωτήρας ανατρεπόταν και τα σφαιρίδια που ήταν τοποθετημένα στην επίπεδη επιφάνειά του έπεφταν σε ένα μεταλλικό κύπελλο (ή πιάτο) προκαλώντας εκκωφαντικό θόρυβο! Όρθιος ο Αριστοτέλης στη στιγμή…
Το ξυπνητήρι του Πλάτωνα
Η πρώτη συσκευή αφύπνισης παγκοσμίως έφερε τη σφραγίδα του σοφού της αρχαιότητας και ξυπνούσε τον Πλάτωνα με σφυρίγματα! Ένα υπερκείμενο κεραμικό δοχείο τροφοδοτούσε μέσω ακροφύσιου ένα δεύτερο δοχείο, αδειάζοντας την προγραμματισμένη χρονική στιγμή με ορμή (μέσω ενός εσωτερικά τοποθετημένου αξονικού σιφωνίου) στο επόμενο κλειστό δοχείο. Ο εγκλωβισμένος αέρας εξερχόταν με πίεση σφυρίζοντας από μια σύριγγα στην κορυφή του.
Μετά τη λειτουργία του μάλιστα το ξυπνητήρι επέστρεφε αυτόματα στην αρχική του κατάσταση, ώστε να επαναρυθμιστεί για την επόμενη αφύπνιση…
Το φορητό ρολόι του Παρμενίωνα
Ένα φορητό δακτυλιοειδές ηλιακό ωρολόγιο έκλεβε όλη τη δόξα στην ελληνική αρχαιότητα. Η λειτουργία του βασιζόταν σε τρεις αρθρωτούς δακτυλίους: ο εξωτερικός ήταν προσανατολισμένος στη διεύθυνση ανατολής-δύσης, ο μεσαίος αποτελούνταν από δύο ημιδακτυλίους που όριζαν τους μήνες για τέσσερα διαφορετικά γεωγραφικά πλάτη (πόλεις δηλαδή) και ο εσωτερικός δακτύλιος διαιρούνταν σε 12 ίσα τμήματα, που όριζαν τις 12 ώρες.
Κατά τη λειτουργία του ρολογιού, ο ημιδακτύλιος με τα δεδομένα της περιοχής στρεφόταν σε θέση 90 μοιρών και ο εσωτερικός δακτύλιος τοποθετούνταν στον σωστό μήνα, οπότε μια φωτεινή κηλίδα έδειχνε την ακριβή ώρα πάνω στην άντυγα! Το πολύ-ρολόι του Παρμενίωνα υπολόγιζε επίσης γεωγραφικά πλάτη, αζιμούθια και ύψη αστέρων…
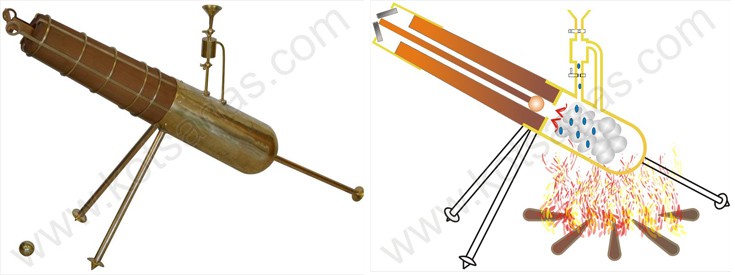
Το ατμοτηλεβόλο του Αρχιμήδη
Ο σπουδαιότερος επιστήμονας της αρχαιότητας, όταν δεν έκανε κολοσσιαίες ανακαλύψεις στους τομείς των μαθηματικών, της γεωμετρίας, της φυσικής, της αστρονομίας, της μηχανικής, της υδραυλικής, της αρχιτεκτονικής και της ναυπηγικής, επινοούσε εφευρέσεις με διαχρονική αξία. Ο υδραυλικός κοχλίας, ο ρωμαϊκός ζυγός, το περίφημο υδραυλικό ωρολόγιο με χτύπους, το αστρονομικό πλανητάριο, τα πανίσχυρα βαρούλκα, η ναυπήγηση της γιγάντιας «Συρακουσίας» και οι φοβερές πολιορκητικές μηχανές είναι μερικά μόνο από τα απίστευτα επιτεύγματά του.
Το ατμοτηλεβόλο εντασσόταν στην πολιορκητική τεχνολογία του και ήταν ένα κανόνι που λειτουργούσε με ατμό! Αποτελούνταν από έναν μεταλλικό κυλινδρικό λέβητα που έφερε πάνω του (συνδεμένο με στρόφιγγα) ένα κλειστό δοχείο με νερό. Ο λέβητας είχε στο ανοιχτό του άκρο μια ενσωματωμένη ξύλινη κάννη, στην οποία τοποθετούνταν η προς εκτόξευση λίθινη σφαίρα. Όταν ο λέβητας αποκτούσε με φωτιά την κατάλληλη θερμοκρασία, ο στρατιώτης άνοιγε τη στρόφιγγα, το νερό έπεφτε στον λέβητα, εξατμιζόταν ταχύτατα, η ξύλινη δοκός έσπαζε και η σφαίρα εκτοξευόταν.
Το βεληνεκές της σφαίρας ρυθμιζόταν από την κλίση του όπλου και την επιλεγμένη αντοχή της ξύλινης δοκού. Το φοβερό και τρομερό ατμοτηλεβόλο του Αρχιμήδη επανασχεδίασε αιώνες αργότερα κανείς άλλος από τον Λεονάρντο Ντα Βίντσι…
Η Κούπα του Δικαίου του Πυθαγόρα
Ο περιβόητος φιλόσοφος και μαθηματικός ήθελε να διδάξει στους μαθητές του τις αρχές του μέτρου στη ζωή, κάνοντάς τους να ζουν με δικαιοσύνη και αρετή. Κι έτσι έφτιαξε ένα διδακτικό κύπελλο που συνόψιζε τη συλλογιστική του. Το «έξυπνο» κύπελλο κρασιού του Πυθαγόρα έφερε μια γραμμή, που καθόριζε το όριο πλήρωσης, και ένα αξονικό ή καμπύλο σιφώνιο. Όταν κάποιος το γέμιζε υπερβολικά, η στάθμη του υγρού κάλυπτε το σιφώνιο και άδειαζε αυτόματα!
Η Κούπα του Δικαίου έλεγε δηλαδή ότι όταν ξεπεράσεις το μέτρο (και διαπράξεις ύβρη), δεν θα χάσεις μόνο αυτά που ξεπέρασαν το όριο, αλλά και όσα είχες αποκτήσει μέχρι τότε…
Ο «υδραυλικός τηλέγραφος» του Αινεία
Οι τηλεπικοινωνίες καθόρισαν και καθορίζουν την τύχη των πολιτισμών και οι αρχαίοι Έλληνες έριξαν μεγάλο βάρος εδώ. Χωρίς τη σπουδαία αυτή γνώση εξάλλου ούτε η εξάπλωση των ελληνικών πόλεων-κρατών σε όλη τη Μεσόγειο ούτε η περίφημη εκστρατεία του Μεγάλου Αλεξάνδρου δεν θα είχαν καρποφορήσει. Ο ελληνικός κόσμος χρησιμοποίησε την απλή πυρσεία (μετάδοση μηνυμάτων με φωτιά) και έφτιαξε ένα εκτεταμένο δίκτυο φρυκτωριών (σταθμών αναμετάδοσης του μηνύματος), αν και δεν έμεινε εκεί.
Η ανάγκη για ταχεία μετάδοση πολλαπλών και διαφορετικών μηνυμάτων οδήγησε τους προγόνους μας στη σύλληψη του «υδραυλικού τηλέγραφου» (4ος αιώνας π.Χ.), μιας εκπληκτικής υδραυλικής συσκευής που απαιτούσε τη χρήση ενός μόνο πυρσού για τη μετάδοση προσυμφωνημένων μηνυμάτων!
Τη μέθοδο περιέγραψε ο Αινείας ο Τακτικός κατά τον 4ο αιώνα π.Χ. στα «Πολιορκητικά» του και όπως μας λέει ο Πολύβιος (στην «Ιστορία» του), ο «υδραυλικός τηλέγραφος» χρησιμοποιήθηκε πρωτίστως για την ταχεία μεταφορά μηνυμάτων στην αχανή αυτοκρατορία του Μεγάλου Αλεξάνδρου. Σε κατάλληλα επιλεγμένα υψώματα λοιπόν, αγγελιοφόροι χρησιμοποιούν ισομεγέθη πήλινα ή μεταλλικά δοχεία με νερό, όπου επιπλέουν πλωτήρες από φελλό λίγο στενότεροι των στομίων, στη μέση των οποίων είναι στερεωμένοι ράβδοι διαιρεμένοι σε ίσα μέρη με αναγραμμένα προσυμφωνημένα μηνύματα, π.χ. «Ήρθαν ιππείς στη χώρα».
Ο χειριστής-«πομπός» δίνει σήμα ανεβάζοντας έναν αναμμένο πυρσό στον χειριστή-«δέκτη» για την αποστολή μηνύματος, περιμένει την ανύψωση του πυρσού του «δέκτη» για επιβεβαίωση και κατόπιν, κατεβάζοντας τον πυρσό, απελευθερώνουν ταυτόχρονα δύο ισομεγέθεις αυλίσκους εκκένωσης των συσκευών τους. Όταν φανεί στη συσκευή του «πομπού» το επιθυμητό μήνυμα, ο χειριστής-«πομπός» ανεβάζοντας τον πυρσό δίνει σήμα στον «δέκτη» για το ταυτόχρονο σταμάτημα της εκροής. Λόγω της ομοιότητας των συσκευών, των στομίων εκροής αλλά και της ίδιας στάθμης του ύδατος, το επιθυμητό προσυμφωνημένο μήνυμα εμφανίζεται στη συσκευή του «δέκτη».
Ο αστρολάβος του Πτολεμαίου
Τα GPS των αρχαίων Ελλήνων ήταν ένα εξαιρετικό αστρονομικό όργανο που απεικόνιζε την ουράνια σφαίρα και χρησιμοποιούνταν για τη μέτρηση του γεωγραφικού μήκους και πλάτους των παρατηρούμενων άστρων από οποιοδήποτε μέρος της Γης, αλλά και για τη μέτρηση της απόστασης Ηλίου-Σελήνης. Αποτελούνταν από επτά ομόκεντρους αρθρωτούς δακτυλίους που έδειχναν μεσημβρινούς, πόλους και ισημερινό, οριζόντιες και κατακόρυφες, την κατεύθυνση του Ηλίου, την ημερήσια περιστροφή της γήινης σφαίρας, τα γεωγραφικά μήκη και πλάτη των αστέρων, ακόμα και τη σκοπευτική διάταξη.
Ήταν ένα πραγματικό αστρονομικό πολυμηχάνημα που συνόψιζε τη γεωγραφική και αστρονομική γνώση Ελλήνων, Βαβυλωνίων κ.λπ. Ο Πτολεμαίος το περιγράφει αναλυτικά στη σπουδαία «Μαθηματική σύνταξη»…
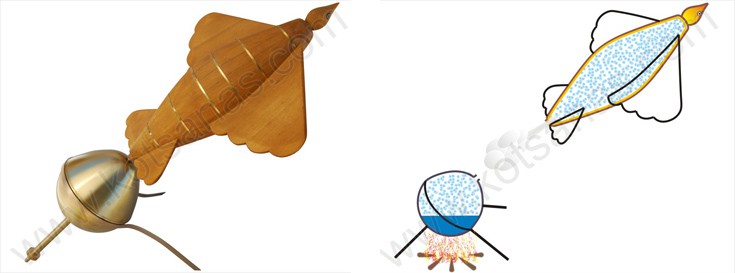
Η «ιπτάμενη περιστερά» του Αρχύτα
Αρχαία ελληνική τεχνολογία χωρίς πτητικές μηχανές δεν γίνεται! Και η ιπτάμενη περιστερά του Αρχύτα του Ταραντίνου ήταν η πρώτη αυτόνομη πτητική μηχανή της αρχαιότητας. Αποτελούνταν από ένα ελαφρύ αλλά στιβαρό κέλυφος που είχε τη μορφή περιστεριού και έφερε εσωτερικά την κύστη ενός μεγάλου ζώου.
Η αεροδυναμική περιστερά ήταν τοποθετημένη με το άνοιγμα της κύστης προσαρμοσμένο στο ανοικτό άκρο ενός θερμαινόμενου στεγανού λέβητα (ή μιας ισχυρής εμβολοφόρας αεραντλίας). Όταν η πίεση του ατμού (ή του αέρα) υπερέβαινε τη μηχανική αντοχή της σύνδεσης, η περιστερά εκτοξευόταν και συνέχιζε την πτήση της για μερικές εκατοντάδες μέτρα με τη βοήθεια της ορμής του εξερχόμενου πεπιεσμένου αέρα της κύστης, σύμφωνα με τις αρχές της αεροδυναμικής !
Πηγή: newsbeast