«Μισώ τα μαθηματικά»

Μισώ τα μαθηματικά

Γιατί μισούμε τα μαθηματικά; Ο Γιώργος Θεοχάρης προτείνει ερμηνείες του (αρχέγονου;) μίσους και επιχειρηματολογεί με όρους αισθητικής υπέρ της κομψότητας των μαθηματικών.

Μικροϊστορίες των επιστημών και της φιλοσοφίας

Ανάμεσα στα γνωστικά πεδία της εγκύκλιας παιδείας, φαίνεται πως τα μαθηματικά έχουν τον υψηλότερο δείκτη απέχθειας. Όλοι έχουμε ακούσει επανειλημμένως τη φράση «μισώ τα μαθηματικά». Υπάρχουν λόγοι να μισεί κανείς τα μαθηματικά; Ασφαλώς! Κατά πρώτον, τα μισεί όποιος μισεί το σχολείο ή/και τη γνώση συνολικά· αυτή η περίπτωση δεν ενδιαφέρει. Δεύτερον, τα μισεί όποιος ήταν τόσο άτυχος ώστε δεν βρέθηκε κατά την εκπαιδευτική του πορεία ούτε ένας εμπνευσμένος δάσκαλος να τον μάθει να τα αγαπάει· η περίπτωση ενδιαφέρει, αλλά εντάσσεται σε ένα πολύ ευρύτερο εκπαιδευτικό πρόβλημα που απαιτεί άλλη κουβέντα από την παρούσα. Τρίτον, τα μισεί όποιος πείστηκε από το (όποιο) περιβάλλον του ότι δεν έχει μυαλό για μαθηματικά – κυρίως τα κορίτσια, από το δημοτικό κιόλας· σε αυτή την κατηγορία των haters (ατάκα των οποίων είναι ο εντός εισαγωγικών προβοκατόρικος και σκοπίμως παραπλανητικός τίτλος) είναι αφιερωμένο (και στοχεύει) το παρόν σημείωμα.

Όταν σε πολύ νεαρή ηλικία βρεθείς αντιμέτωπος με την κυρίαρχη (ακόμα και τώρα, σήμερα) αντίληψη ότι τα μαθηματικά (και οι θετικές επιστήμες γενικότερα) είναι «αντρική» υπόθεση, είναι φυσικό να τα μισήσεις, αν είσαι κορίτσι. Αλλά και αγόρι να είσαι, αν σε πείσουν ότι δεν τα «παίρνεις» τα μαθηματικά, πάλι θα τα μισήσεις. Και όμως, οι πάντες μπορούν να κάνουν μαθηματικά, ως ένα βαθμό. Δεν υπάρχει αμφιβολία ότι για να κάνεις μαθηματικά υψηλού επιπέδου, χρειάζεται ταλέντο (ό,τι κι αν σημαίνει αυτό). Κάποιοι άνθρωποι είναι γεννημένοι για τα μαθηματικά, αλλά αυτό δεν σημαίνει ότι όλοι οι υπόλοιποι πρέπει να αποθαρρύνονται από την ενασχόλησή τους με αυτά (στον βαθμό που τους αναλογεί, πάντα· δεν γίνεται να ζητάς από μια γάτα να γαβγίσει) και να στερηθούν έτσι τη χαρά (ναι, τη χαρά!) που μπορούν να αντλήσουν από εκεί. Δεν χρειάζεται να έχεις το ταλέντο του Αρχιμήδη, του Newton, του Euler ή του Gauss (για πολλούς, οι κορυφαίοι των κορυφαίων) για να κάνεις μαθηματικά· αν ήταν έτσι, τα μαθηματικά θα ήταν ένα γνωστικό πεδίο για τους ελάχιστους, τους «εκλεκτούς» – αλλά δεν είναι· καταρχήν, όλοι (κι εδώ κυριολεκτώ) μπορούν να κάνουν κάποια μαθηματικά. Επίσης, είναι από τις επιστήμες που δεν σου ζητάει να επενδύσεις παρά μόνο χαρτί και μολύβι· και φαιά ουσία. Τέλος, μέσα από τη μαθηματική σκέψη (ανεξαρτήτως επιπέδου) είναι στατιστικά εξακριβωμένο ότι ο άνθρωπος βελτιώνεται σε κάθε τομέα του επιστητού, σχετικού και άσχετου. Μεγάλη κουβέντα θα πω, αλλά θα την πω γιατί την πιστεύω: τα μαθηματικά (όπως και κάθε είδους γνώση) σε κάνουν καλύτερο άνθρωπο.

Δεν θα επιχειρηματολογήσω υπέρ της εύκολα αποδείξιμης χρησιμότητας των μαθηματικών (το έχω κάνει στο πρόσφατο παρελθόν – βλ. εδώ)· αντίθετα, θα τα υποστηρίξω θεωρώντας τα παντελώς άχρηστα για την καθημερινή ζωή, όπως δηλαδή πιστεύουν οι περισσότεροι. Θα τα υποστηρίξω για αυτά καθ’ εαυτά, αγνοώντας την αδιαμφισβήτητη χρησιμότητά τους. Θα τα υποστηρίξω γιατί είναι αδικημένα στο μυαλό μυριάδων μαθητών διαχρονικά (και χωρίς να φταίνε γι’ αυτό ούτε οι μαθητές ούτε τα μαθηματικά). Θα τα υποστηρίξω αισθητικά.

Καταρχάς, τα μαθηματικά έχουν ένα πλεονέκτημα: την απόδειξη. Όταν ισχυρίζεσαι κάτι, πρέπει να το αποδείξεις – καλύτερα: σου προσφέρονται τα εργαλεία, έχεις τηδυνατότητα να το αποδείξεις. Φυσικά, υπάρχουν προβλήματα που παραμένουν άλυτα, αλλά είναι θέμα χρόνου (σε μερικές περιπτώσεις πολύ χρόνου) να λυθούν. Και βέβαια, όταν μιλάμε για αποδείξεις, δεν πρέπει να ξεχνάμε και τις αρνητικές αποδείξεις, εκείνες δηλαδή που αποδεικνύουν ότι κάτι δεν ισχύει (λ.χ., το Θεώρημα της Μη Πληρότητας του Gödel) – και αυτές αποδείξεις είναι, και μάλιστα σημαντικότατες. Σ’ αυτό το σημείο ίσως αντιτείνει κάποιος ότι όλες οι επιστήμες, λίγο-πολύ, κάνουν χρήση της απόδειξης. Σύμφωνοι, αλλά όχι με τον κατηγορηματικό τρόπο των μαθηματικών (για να μην αναφέρω καν ότι ως προς τη χρήση της απόδειξης προηγούνται και χρονικά των άλλων επιστημών). Τα μαθηματικά δεν χρησιμοποιούν την απόδειξη με τον τρόπο που τη χρησιμοποιεί, λ.χ., η ιστορία, τα οικονομικά ή οι πολιτικές επιστήμες (και ούτε λόγος για «επιστήμες» όπως η κοινωνιολογία ή η ψυχολογία – ούτε και για τη φιλοσοφία, η οποία, αν μη τι άλλο, δεν διεκδικεί επιστημονικές δάφνες)· η μαθηματική απόδειξη είναι ρητή και κατηγορηματική: αν αποδειχτεί σωστή, δεν επιδέχεται αμφισβήτηση. «Έτσι έχουν τα πράγματα και ορίστε η απόδειξη». Τελεία και παύλα.

Ενίοτε δε, η μαθηματική απόδειξη είναι κομψή. Εδώ, στο αισθητικό κομμάτι, αξίζει να σταθώ λιγάκι παραπάνω. Ακόμα κι αν κάποιος παραμένει παράλογα αμετάπειστος ως προς τη χρησιμότητα των μαθηματικών, θα ήθελα να τον αναγκάσω να παραδεχτεί, κατ’ ελάχιστον, ότι κάποιες αποδείξεις είναι όμορφες. Αυτό είναι από μόνο του χρήσιμο (γιατί αν δεν είναι, τότε η μπάλα της ισοπέδωσης θα πάρει και τις καλές τέχνες!) Για να καταστήσω απολύτως σαφές το επιχείρημα της αισθητικής χαράς, θα χρησιμοποιήσω ένα κλασικό παράδειγμα από την ιστορία των μαθηματικών: την απόδειξη του Ευκλείδη για την ύπαρξη απείρου πλήθους πρώτων αριθμών. Για να συνεννοηθούμε, θα χρειαστεί να δώσω τους ορισμούς των πρώτων και των σύνθετων, αλλά –κατά τα άλλα– η απόδειξη είναι φιλική προς τους πάντες, ανεξαρτήτως μαθηματικής προπαιδείας. Άλλωστε, όπως ήδη ειπώθηκε, ο φιλόδοξος στόχος του παρόντος είναι να μεταπείσει όσους μισούν τα μαθηματικά. Για να δούμε…

Ως πρώτος ορίζεται ένας φυσικός αριθμός (όπου φυσικοί είναι οι ακέραιοι πλην του 0) μεγαλύτερος της μονάδας που έχει την ιδιότητα οι μόνοι φυσικοί διαιρέτες του να είναι η μονάδα και ο εαυτός του.

Ένας φυσικός αριθμός μεγαλύτερος της μονάδας που δεν είναι πρώτος ονομάζεται σύνθετος. Π.χ., ο αριθμός 3 είναι πρώτος, επειδή διαιρείται μόνο από το 1 και το 3, ενώ ο 4 είναι σύνθετος επειδή διαιρείται, εκτός από το 1 και το 4, και από το 2.

(Το 0 και το 1 δεν είναι πρώτοι αριθμοί. Το 0 συχνά δεν θεωρείται καν φυσικός αριθμός, ενώ για το 1 υπάρχουν τεχνικοί λόγοι που μας αναγκάζουν να μην το θεωρούμε πρώτο αριθμό.).

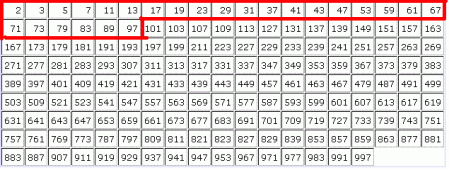
Η ακολουθία των πρώτων μέχρι το 100 είναι η εξής:

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97

Όπως είναι φανερό, ο αριθμός 2 είναι ο μόνος ζυγός πρώτος αριθμός (γιατί όλοι οι υπόλοιποι ζυγοί, οι μεγαλύτεροι του 2, διαιρούνται, εκτός από το 1 και τον εαυτό τους, και από το 2 – τουλάχιστον). Συνεπώς, όλοι οι άλλοι πρώτοι αριθμοί είναι μονοί.

Ευκλείδη Στοιχεία, απόσπασμα παπύρου του Οξυρύγχου, 1ος αι. μ.Χ.

Αυτά φτάνουν για να περάσουμε στην απόδειξη του Ευκλείδη για την ύπαρξη απείρου πλήθους πρώτων αριθμών, η οποία βρίσκεται στο Βιβλίο IX, Πρόταση 20 των Στοιχείωνi (3ος αιώνας π.Χ.). Ο Ευκλείδης στα Στοιχεία του είχε συγκεντρώσει περίπου όλη τη μαθηματική γνώση μέχρι και την εποχή του, συνεπώς δεν είναι απολύτως βέβαιο ότι η απόδειξη είναι δική του· από την άλλη, δεν υπάρχει κάποιος ιδιαίτερος λόγος να υποθέσουμε ότι δεν είναι δική του. Αυτό όμως μικρή σημασία έχει· εκείνο που είναι σημαντικό είναι η ίδια η απόδειξη. Δεν θα την παραθέσω κατά λέξη γιατί η γλώσσα του Ευκλείδη ξενίζει τον σύγχρονο αναγνώστη, ακόμα και σε μετάφραση· θα προτιμήσω μία διασκευή, αλλά η ουσία –εγγυημένα– παραμένει η ίδια.

Πρέπει να αποδείξουμε ότι οι πρώτοι είναι άπειροι. Προς τούτο, ας υποθέσουμε ότι δεν είναι άπειροι, και ότι η πλήρης ακολουθία των 2, 3, 5 κ.λπ. τελειώνει στον αριθμό P, τον μεγαλύτερο πρώτο.

Με αυτή την υπόθεση κατά νου, ας θεωρήσουμε έναν αριθμό Q ο οποίος ορίζεται ως εξής:

Q = (2·3·5· … ·P) +1

Τώρα, υπάρχουν δύο δυνατότητες, σε ό,τι αφορά τον Q: είτε είναι πρώτος είτε δεν είναι.

Αν είναι πρώτος, τότε έχουμε ήδη βρει έναν πρώτο αριθμό που είναι σαφώς μεγαλύτερος από τον P, για τον οποίο είχαμε υποθέσει ότι είναι ο μεγαλύτερος πρώτος (δηλαδή, ο τελευταίος της ακολουθίας).

Αν, όμως, δεν είναι πρώτος; Δεν γίνεται να μην είναι πρώτος. Και να γιατί:

Οι πρώτοι είναι το υλικό με το οποίο χτίζονται όλοι οι αριθμοί μέσω πολλαπλασιασμού, και μάλιστα με τρόπο μοναδικό (θεώρημα που επίσης περιέχεται στα Στοιχεία: Βιβλίο IX, Πρόταση 14, σε συνδυασμό με Βιβλίο VII, Προτάσεις 30 & 32): λ.χ., ο αριθμός του κτήνους, το 666 = 2·3·3·37 (όλοι πρώτοι). Αυτό σημαίνει ότι κάθε αριθμός διαιρείται από έναν τουλάχιστον πρώτο (συνήθως, προφανώς από περισσότερους). Εντούτοις, ο Q, διαιρούμενος από τον κάθε πρώτο ξεχωριστά, μέχρι και τον P, τον υποτιθέμενο μεγαλύτερο πρώτο, αφήνει πάντα υπόλοιπο 1. Με άλλα λόγια, ο Qείναι πρώτος, γιατί διαιρείται μόνο από τη μονάδα και τον εαυτό του. Ναι, αλλά εμείς είχαμε υποθέσει ότι ο P είναι ο μεγαλύτερος πρώτος και τώρα βλέπουμε ότι ο Q, που είναι σαφώς μεγαλύτερος από τον P, είναι κι αυτός πρώτος. Άρα η αρχική μας υπόθεση –ότι ο P είναι ο μεγαλύτερος πρώτος– είναι εσφαλμένη. Κι αφού μπορούμε ανά πάσα στιγμή να παράγουμε έναν πρώτο μεγαλύτερο από οποιονδήποτε άλλον πρώτο, έχουμε αποδείξει ότι οι πρώτοι είναι άπειροι.

Μαγεία! Αν αυτή η απόδειξη δεν είναι ο ορισμός της κομψότητας, τότε δεν ξέρω τίποτα για τη συγκεκριμένη έννοια.

Γράφει σχετικά ο σπουδαίος μαθηματικός G.H. Hardy, απολύτως γοητευμένος: «Η απόδειξη έγινε με εις άτοπον απαγωγή, και η εις άτοπον απαγωγή, που ο Ευκλείδης αγαπούσε τόσο πολύ, είναι ένα από τα ωραιότερα όπλα του μαθηματικού. Είναι πιο όμορφο από οποιοδήποτε σκακιστικό γκαμπίii. Ένας σκακιστής μπορεί να θυσιάσει ένα πιόνι, ή ακόμα και ένα κομμάτι, αλλά ο μαθηματικός προσφέρει το ίδιο τοπαιγνίδι».iii Έτσι ακριβώς!

Όπως είδατε, δεν χρειάστηκαν τίποτα τρομερά μαθηματικά στον Ευκλείδη για να αποδείξει την απειρία των πρώτων και να προσφέρει στην ανθρωπότητα ένα κομψοτέχνημα! Βέβαια, δεν είναι όλες οι αποδείξεις τόσο συγκλονιστικές μέσα στην ιδιοφυή τους απλότητα· υπάρχουν αποδείξεις που όντως απαιτούν τρομεράμαθηματικά και που τραβάνε σε μάκρος δυσθεώρητο. Εντούτοις, σε πρώτο επίπεδο, τα μαθηματικά, καίτοι η αυστηρότερη των επιστημών, έχουν μια χάρη ανυπέρβλητη. Σκέφτομαι όλα εκείνα τα παιδιά, αγόρια και κορίτσια (και περιττό να πω ότι τα κορίτσια είναι, διανοητικά μιλώντας, εξίσου εξοπλισμένα με τα αγόρια για να κάνουν μαθηματικά – ελπίζω ότι αυτό τουλάχιστον είναι πλέον αυταπόδεικτο) που ωθήθηκαν να μισήσουν τα μαθηματικά και θλίβομαι. Σκέφτομαι τη χαρά που απώλεσαν λόγω ενός ευεξήγητου μεν, απαράδεκτου δε, μίσους· την πνευματική χαρά – γιατί τα μαθηματικά είναι, καταρχήν, ένα πνευματικό παιχνίδι. Σκέφτομαι ότι αν είχε βρεθεί στον δρόμο τους ένας χαρισματικός εκπαιδευτικός (ή γονιός), ικανός να τους εμφυσήσει την αγάπη του για την επιστήμη, θα είχε αλλάξει, έστω και κατά τι, έστω και απειροελάχιστα, η ζωή τους προς το καλύτερο. Αλλά μη μασάτε: ποτέ δεν είναι αργά!

i Τα Στοιχεία (ή Στοιχείωσις, όπως ήταν στην πραγματικότητα ο τίτλος του) του Ευκλείδη είναι το πιο φημισμένο σύγγραμμα στην ιστορία των μαθηματικών και ένα από τα μεγαλύτερα επιτεύγματα της παγκόσμιας γραμματείας. Μόνο ηΒίβλος το ξεπερνάει σε αριθμό εκδόσεων. Πρόκειται για το βιβλίο που έμαθε τον κόσμο (κυριολεκτικά: τον κόσμο όλο) γεωμετρία. Αποτελείται από 13 “βιβλία” (κεφάλαια), μεταξύ των οποίων τα VII–IX περιέχουν τη θεωρία των αριθμών. Για όποιον ενδιαφέρεται, ολόκληρο το έργο σε σχολιασμένη μετάφραση (πρόκειται για την τρίτομη έκδοση του 2001 από το Κέντρο Έρευνας Επιστήμης και Εκπαίδευσης), βρίσκεται στο Διαδίκτυο.

ii Γκαμπί: σκακιστικός όρος για τη “θυσία” κομματιού που όμως επιφέρει πλεονέκτημα.

iii G.H. Hardy, Η Απολογία ενός Μαθηματικού, μετάφραση: Δημήτης Καραγιαννάκης & Μιχάλης Λάμπρου, Πανεπιστημιακές Εκδόσεις Κρήτης, Ηράκλειο 1993, σ. 69.